Fonction dérivée
Fonction dérivée
Seul le calcul préalable du coefficient directeur de la tangente permet d'obtenir un tracé correct. Ce coefficient directeur s'appelle le nombre dérivé. Pour le calculer, on peut déterminer la fonction dérivée en utilisant les règles de dérivation.
Quand on détermine le sens de variation de la fonction, on peut, au lieu d'observer si les images sont dans le même ordre que les valeurs de la variable, considérer le signe du coefficient directeur de la tangente en tout point de sa représentation graphique : on fait alors l'étude du signe de la dérivée
m = (yB - yA) / (xB - xA)
Lorsque B se rapproche de A, ce coefficient directeur se rapproche, en général, d'une valeur limite. On dit alors que la fonction est dérivable en x = a et on appelle cette limite : nombre dérivé de f en a. On le note f'(a).
Fonctions de référence
Une fonction est dérivable sur un intervalle I si sa courbe admet, en tout point dont l'abscisse est dans I, une tangente, c'est-à-dire une droite que l'on peut confondre avec la courbe si l'on est suffisamment près du point de contact. Ce qui se dit aussi : f est dérivable sur I si f est dérivable en tout réel x de I.
La fonction dérivée de f, notée f' est la fonction qui, à tout réel x de I, associe le nombre dérivé f'(x)
Fonction affine -
Les fonctions affines sont dérivables sur . Leur dérivée est une fonction constante, égale à leur coefficient directeur.
Si f(x) = ax + b alors on a f'(x) = a
Fonction constante -
On remarque que les fonctions constantes ont une dérivée nulle. On peut mémoriser ce résultat en pensant qu'en tout point une droite est sa propre tangente.
Si f(x) = n alors on a f'(x) = 0
Fonction puissance -
Les dérivées des fonctions puissances, inverse et racine se calculent à l'aide de la formule générale :
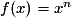
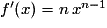
On en déduit alors que :
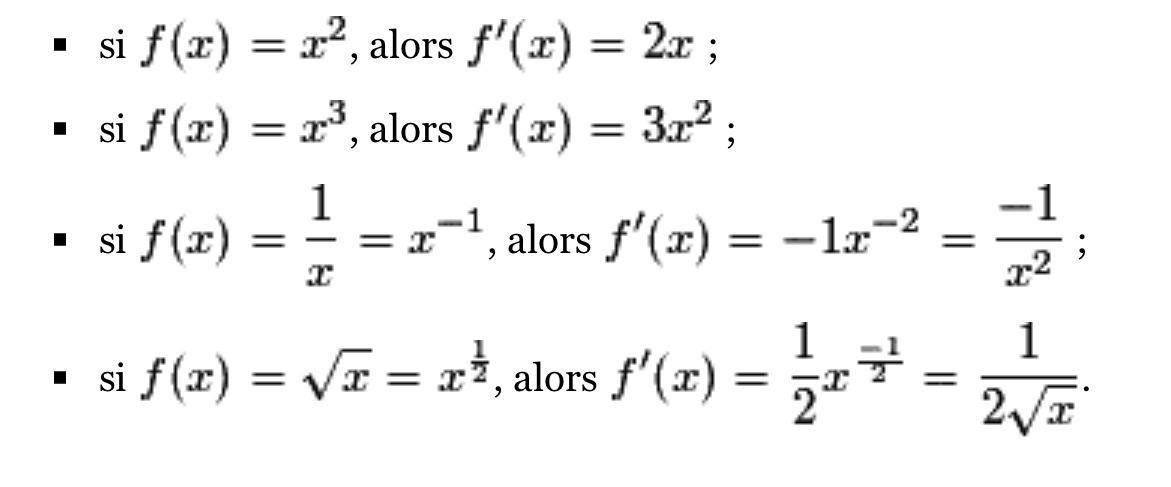
Remarque : Attention : les fonctions carré, cube et inverse sont dérivables sur leur ensemble de définition. Ce n'est pas le cas pour la fonction racine, qui est définie en 0, mais qui n'est pas dérivable en ce point.
Dériver une fonction définie comme une somme, un produit, un quotient ou une composée de deux fonctions
La dérivée de la somme de deux fonctions se calcule très simplement :
Si on a f = u + g alors f' = u' + g'
Il en est de même pour le produit d'une fonction par un réel :
Si on a f = ku alors f' = ku'
Pour le produit ou le quotient de deux fonctions, on identifie d'abord les fonctions f et g pour en calculer préalablement les dérivées. Il suffit alors de remplacer dans l'une des formules.
Si on a f = uv alors f' = u'v + v'u
Si on a f = u / v alors f' = (u'v - uv') / v²
Déduire le sens de variations d'une fonction
En grossissant suffisamment le voisinage du point de contact de la courbe et de sa tangente, on vérifie que les deux tracés sont très proches l'un de l'autre. Le sens de variation de la fonction est alors le même que celui de la fonction affine représentée par la tangente.
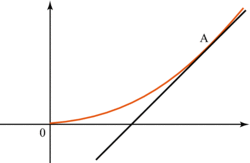
On en déduit que, sur un intervalle I :
- Si f'(x) > 0, alors la fonction f est strictement croissante ;
- Si f'(x) < 0, alors la fonction f est strictement décroissante
- Si f'(x) = 0, alors la fonction f est constante