Trigonométrie - Propriétés
La mesure en radian d'un angle est proportionelle à sa mesure en degré car π = 180°
Pour trouver la mesure en degré d'un radian on calcule :
[180 x (radian)] / π
Pour trouver la mesure en radian d'un angle en degré on calcule :
[(angle en degré) x π ] / 180
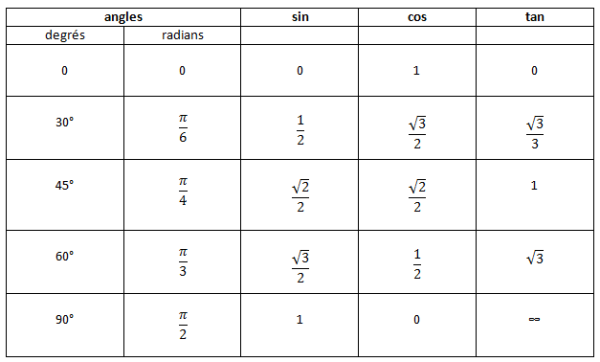
Angles à connaître par coeur :
- 0° = 0 radian
- 30° = π/6
- 45° = π/4
- 60° = π/3
- 90° = π/2
Propriétés à savoir par coeur : (on note u! vecteur u et v! vecteur v)
- (u! ; v!) = -(v! ; u!)
- (u! ; -v!) = (u! ; v!) + π
- (-u! ; -v!) = (u! ; v!)
Pour determiner le radian d'un angle, on l'exprime en fonction du vecteur OI!
exemple : (OA! ; OB!) = (OA! ; OI!) + (OI! ; OB!) = -(OI! ; OA!) + (OI ; OB!)
Propriétés à savoir par coeur :
- cos (α) = cos (-α)
- sin (α) = -sin (-α)
- cos (π + α) = -cos (α)
- sin (π + α) = -sin (α)
- cos (π - α) = -cos (α)
- sin (π - α) = sin (α)
- cos (π/2 - α) = sin (α)
- sin (π/2 - α) = cos (α)
- cos (π/2 + α) = - sin (α)
- sin (π/2 + α) = cos (α)
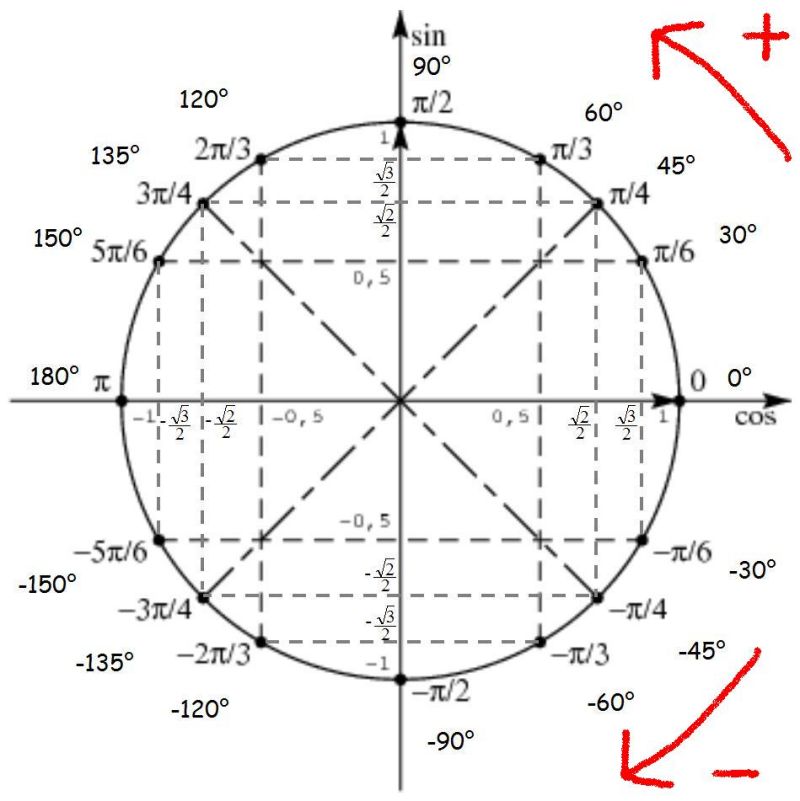
Cosinus et Sinus des angles à connaître par coeur :
Détermination d'un angle x
On cherche à obtenir le cas de figure suivant :
- cos x = cos a
- sin x = sin a
Deux solutions :
Si cos x = cos a
Alors :
- x = a + 2kπ
- x = -a + 2kπ
Avec k entier relatif
Si sin x = sin a
Alors :
- x = a + 2kπ
- x = π - a + 2kπ
Avec k entier relatif
Dans un intervalle I donné, on remplace k par un entier relatif pour vérifier si x ∈ I donné
Exemple -
On cherche x sachant que cos x = 1/2 dans l'intervalle I [ 0 ; 2π]
On a cos x = 1/2
Or on sait que l'angle a dont le cosinus vaut 1/2 est l'angle a = π / 3
d'où : cos x = cos π / 3
ce qui équivaut à :
- x = π / 3 + 2kπ
- x = - π / 3 + 2kπ
pour k = 0 on obtient :
- x = π / 3
- x = -π / 3
pour k = 1 on obtient :
- x = π / 3 + 2π = 7π / 3
- x = -π / 3 + 2π = 5π / 3